2F53
|
Created in Jan.2015 2F53 is a study on recursive geometry subdivision using Bézier curves, and is later developed and integrated into the generative visual system I designed for Karma Fields’s Debut.
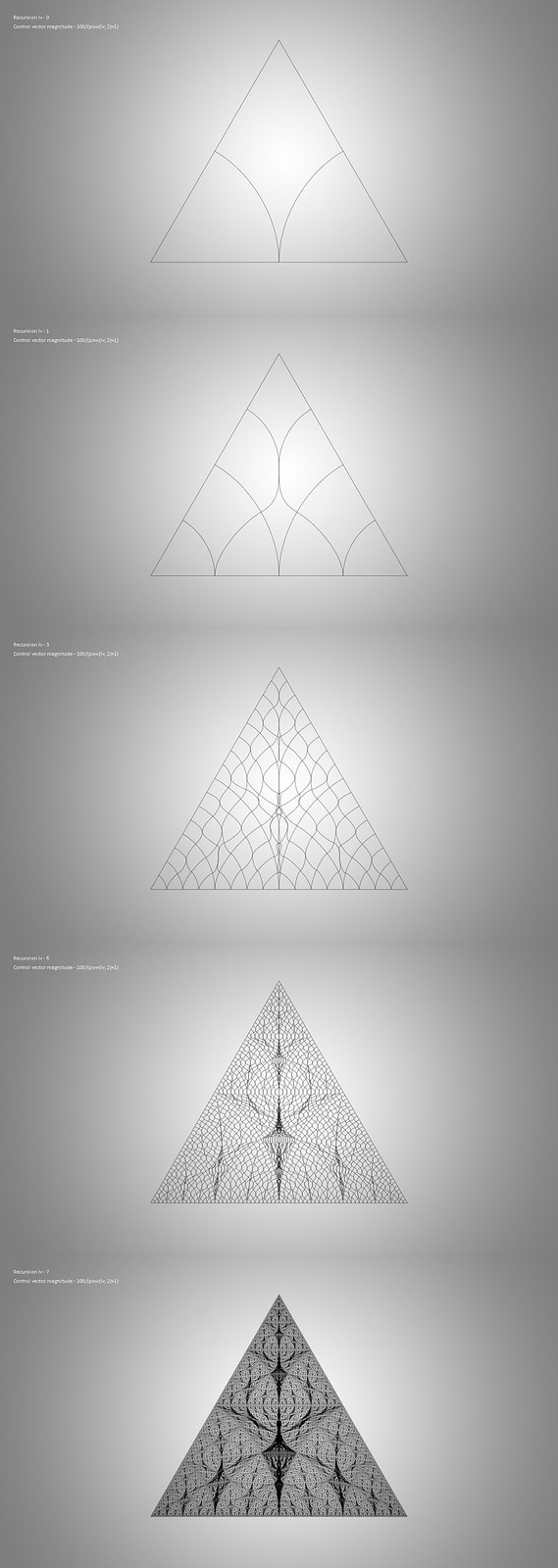
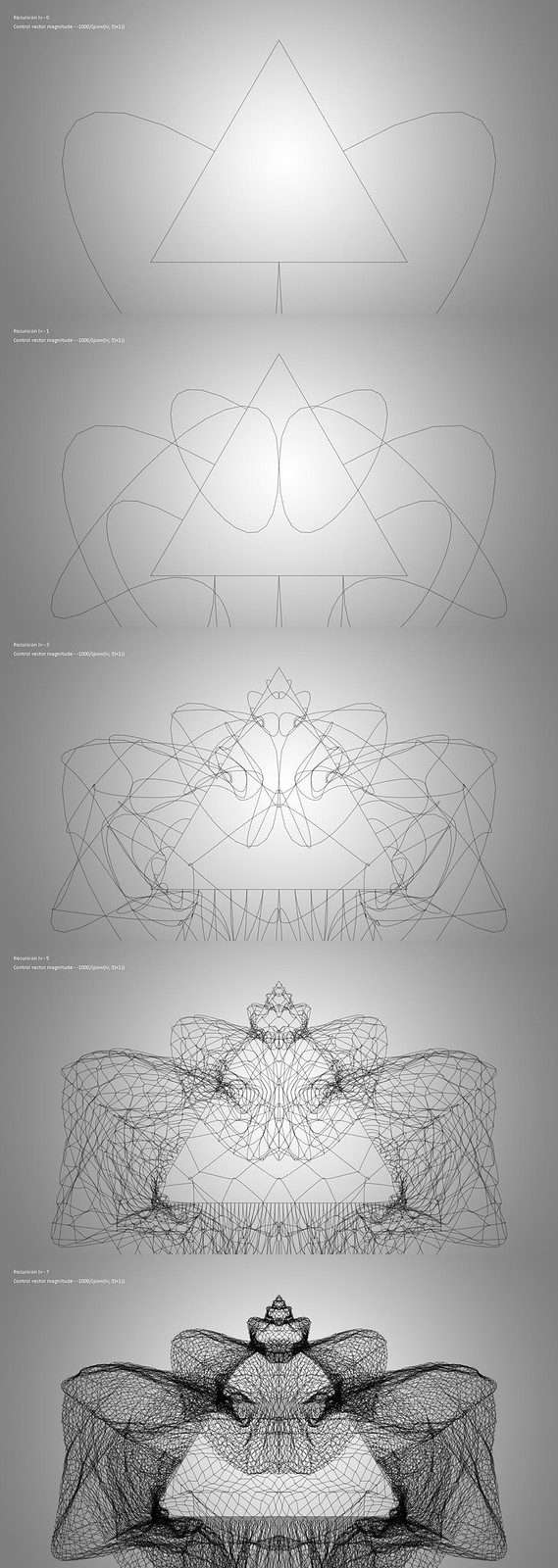
针对中国用户,若上部视频无法显示,可以访问土豆网版本。 Each tile of the structure consists of three bound vertices + three invisible edges (line segments or Bézier curve segments according to location of the tile within the root triangular framework); three mid vertices (each for one edge) + three control vertices (each corresponding to one mid vertex for generating the inner division) + two visible Bézier curve segments for subdivision. Unlike 115C8 or 1194D, the bound edges for each tile are not individually created within the recursion. The improved algorithm re-uses the forming edges on the root level, and simply takes in start and end interpolation positions, together with its own relative interpolation to compute and generate its children tiles. The 3D protrusion implemented in 18F44 is later integrated to add more visual complexity.
Control vector magnitude: pow(lv,1.0/3)+1
Control vector magnitude: 100/(pow(lv, 2)+1)
Control vector magnitude: -1000/(pow(lv, 3)+1))
|